Perspectives and Code - Redesigning Fibonacci
Among the first few coding challenges a newbie comes across is that of computing the Fibonacci Sequence. At a glance, this absurdly random question does not appear to offer any real world use case (despite it’s importance), apart from the fact that it’s used to demonstrate the concepts of recursion to new programmers.
A good use-case of the Fibonacci sequence that is not so popular is to explain concepts of algorithmic complexity. So, lets begin by looking at the definition of the so called sequence.
0 1 1 2 3 5 8 13 . . . .
As the above image shows, every n’th element of the sequence is the sum of the previous 2 elements i.e Fib(n) = Fib(n-1) + Fib(n-2). Most of us who are familar with the concepts of recursion typically come up with a simple recursive algorithm to solve this problem.
def fib1(n): if n == 0: return 0 if n == 1: return 1 return fib1(n-1) + fib1(n-2)
Now lets analyze the above solution. Lines 2 and 3 together take up O(1) time. Let T(n) represent the number of steps taken for the function fib1(n) to compute a result. The return statement at line 4 has a time complexity of T(n-1) + T(n-2). So overall, the time complexity of fib1 can be represented as follows: T(n) ≤ O(1) + T(n-1) + T(n-2). This formula looks similiar to that of the original definition of fibonacci numbers, except for the addition of a constant term O(1).
Hence, it can concluded that the time complexity for n numbers is atleast as large as the n'th Fibonacci number. T(n) ≥ Fib(n)
We all know that fibonacci numbers grow exponentially in a constant φ, where φ equals (1+√5)/2 which approximates to 1.61803 (aka the golden ratio). This is bad because our algorithm is now exponential in time complexity which makes it very slow. To put things into perspective lets plot the execution time of fib1(n) for increasing values of n.
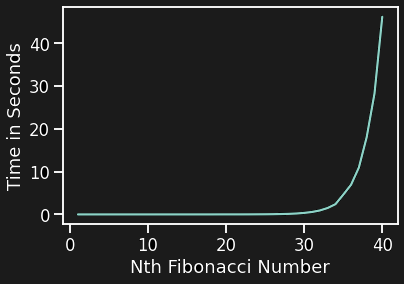
As the plot shows, beyond a certain point the function takes a very large time to compute a result (approx 40 seconds to compute the value for fib1(40)). The reason behind these huge computation times can be visualized easily using the above tree which represents how the recursive algorithm works
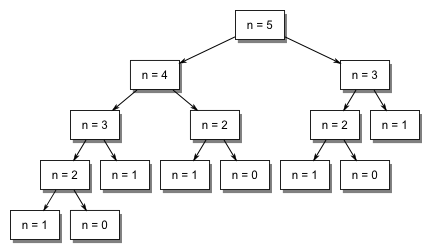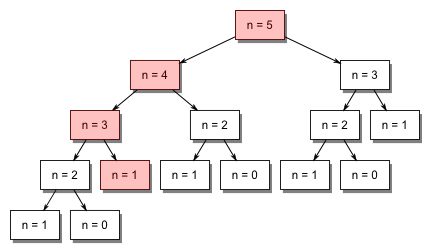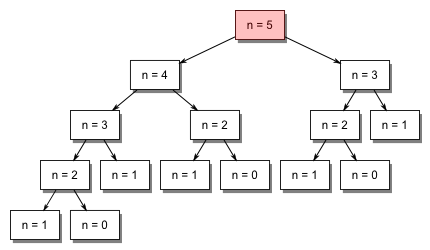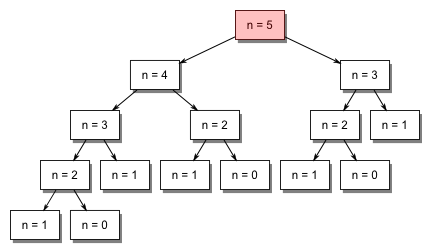
It becomes evident from the above image that the solution for smaller subproblems gets computed more than once (eg: n=1 in the above tree), sometimes an exponential number of times. This is the root cause of the inefficiencies seen in this method of computing the fibonacci sequence.
What if we computed each sub-problem exactly once, and use previously computed values to arrive at the answer using a bottom-up approach. This programming methodology is known as dynamic programming. For our particular problem, we store the results for each n’th term in an array and use this array to compute the value for the (n+1)’th term.
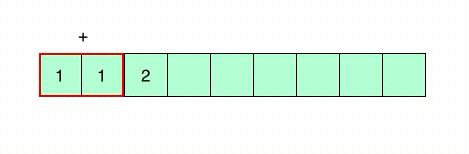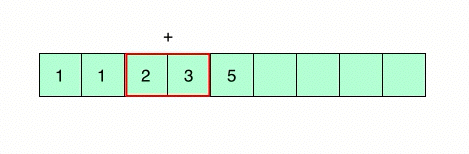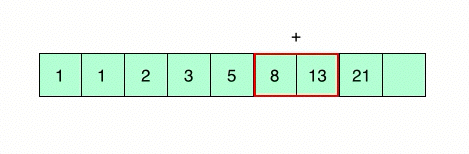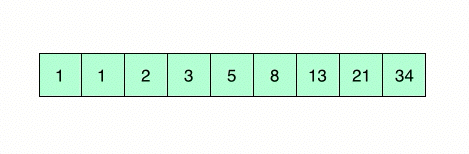
Programming the above mentioned algorithm:
def fib2(n): if n == 0: return 0 if n == 1: return 1 fib_list = [None] * (n+1) fib_list[0] = 0 fib_list[1] = 1 for i in range(2,n+1): fib_list[i] = fib_list[i-1] + fib_list[i-2] return fib_list[n]
We can see that the base case (lines 2-6) take up O(1) in time complexity. The for loop at lines 7-8 has a time complexity of O(n). Hence the new approach has a net time complexity of approximately O(n). This is a huge improvement from the exponential time complexity seen in our first recursive implementation. Plotting the execution times for fib2(n) we get:
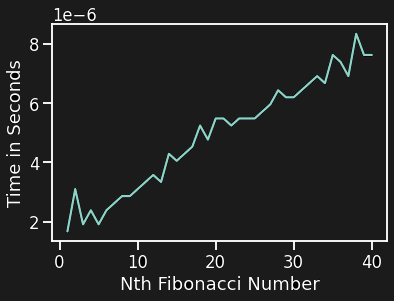
We can see an almost linear plot in the above figure. Also note that computing the 40th fibonacci number takes around 8x10-6 seconds whereas the initial recursive implementation took 40 seconds for the same value of n, a very huge leap in performance.
This is a great example of how minor changes in perspective of how code is implemented can bring significant benefits in terms of performance.
This post was inspired by Module-1 of Udacity’s Intro to Graduate Algorithms Course