Building a Perceptron from Scratch in Python

27 Oct 2024

The perceptron, also known as the ‘artificial neuron’, ‘single-layer perceptron’, etc is often termed as the structural building block of deep learning. But before we look into the logic, and code for implementing one, let’s first take a peek at its biological counterpart: the neuron. If you want to skip the theoretical jargon, you can go straight to the implementation over here.

Structure of a Typical Neuron

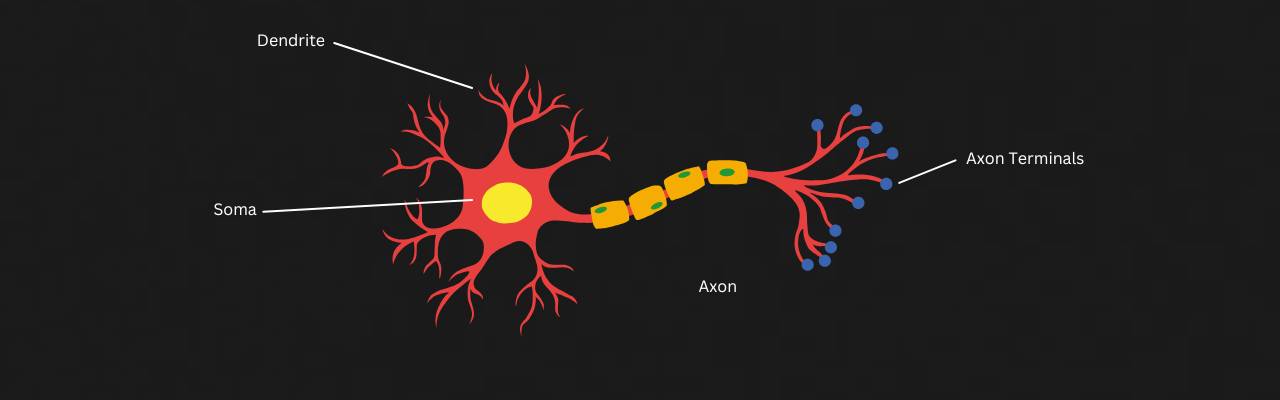
A typical neuron consists of several dendrites that receive signals from other neurons or receptors. These signals are sent to the soma, where most protein synthesis occurs. The processed signal then travels down the axon and is transmitted to other receptors through synapses at the axon terminals. The interconnection of millions of these basic neurons enables complex species like ours to think, breathe, and navigate this Earth.

The Perceptron

The Perceptron Model and Simplified Equation

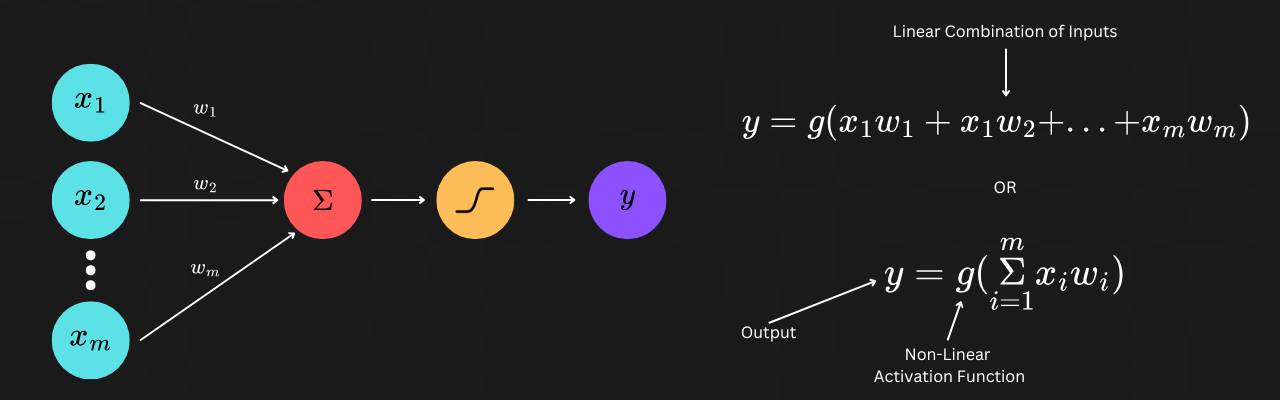
A perceptron can be seen as an attempt to recreate the functionality of a neuron at a higher level. (there has been recent strides on implementing this at a much lower level.)

As seen in the figure above, we have inputs x₁ to x_m which are multiplied by a set of weights w₁ to w_m. I like to think of each weight as a preference or sensitivity the neuron has to the value of its corresponding input. The weighted sum of each input with its corresponding weight (x₁w₁ + x₂w₂ + … + x_mw_m), is then passed onto a non-linear activation function before yielding the final output. Now why is this step required?

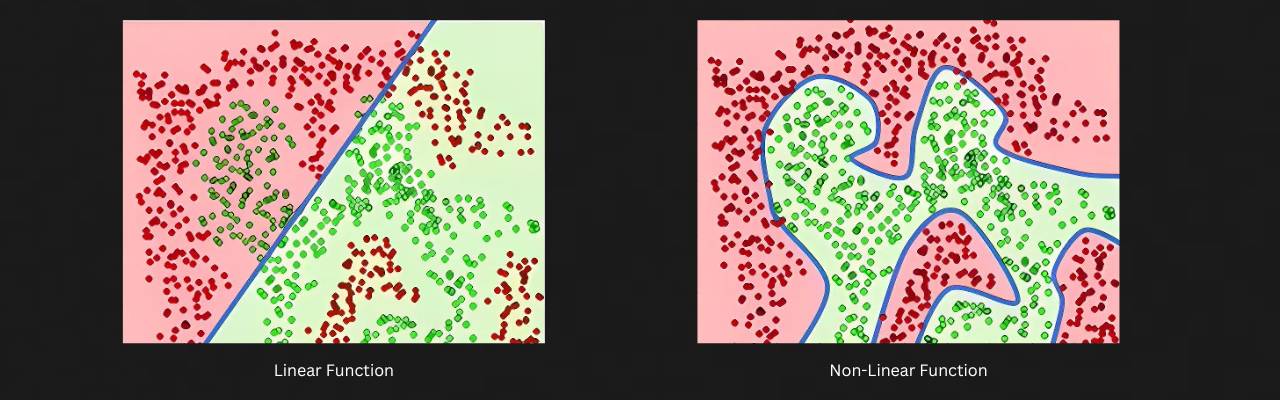
The weighted sum of inputs multiplied with their corresponding weights is ultimately just a linear function. This means that no matter how many perceptrons or layers you add, the final output will still represent a line. However, most real-world scenarios are non-linear and cannot be separated with just a line. This is why an activation function is crucial for a perceptron or neural networks in general.

Effect of Activation Function on Non-Linear Data

There’s one missing piece in the equation we haven’t covered yet: the bias term, or bias weight, whichever you prefer. What this enables is for our perceptron to shift its activation output left or right along the horizontal axis. This allows the perceptron to better fit the data and enables it to provide signals even when all inputs are zero. The following stackoverflow question throws in a few examples and perspectives on the effect of bias in the performance of a perceptron. Given this info, the updated equation of a perceptron looks like this:

The Perceptron Model and its Equation

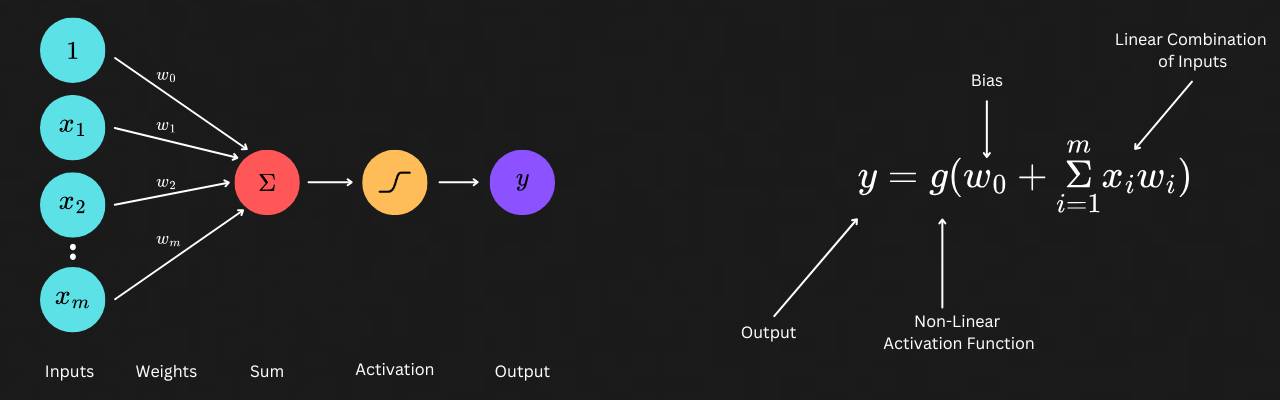
With this we now have a foundation on how a perceptron is able to convert inputs into outputs along with a mathematical representation of the same. But this paves way to a new question. . .

How do we set the weights?

Before we talk about how weights are decided, another term needs to be visited: the loss function. A loss function is essentially a measure on how far the predicted output of a model is from the expected output. There are many loss functions, such as MSE, RMSE, and MAE, which all, in essence, provide a metric of how far the predicted output is from the actual output. In an ideal scenario, for all possible inputs, the weights of the perceptron should produce an output that is closest (with the lowest loss) to the expected answer.

Loss function calculates the distance between your target and predicted outputs

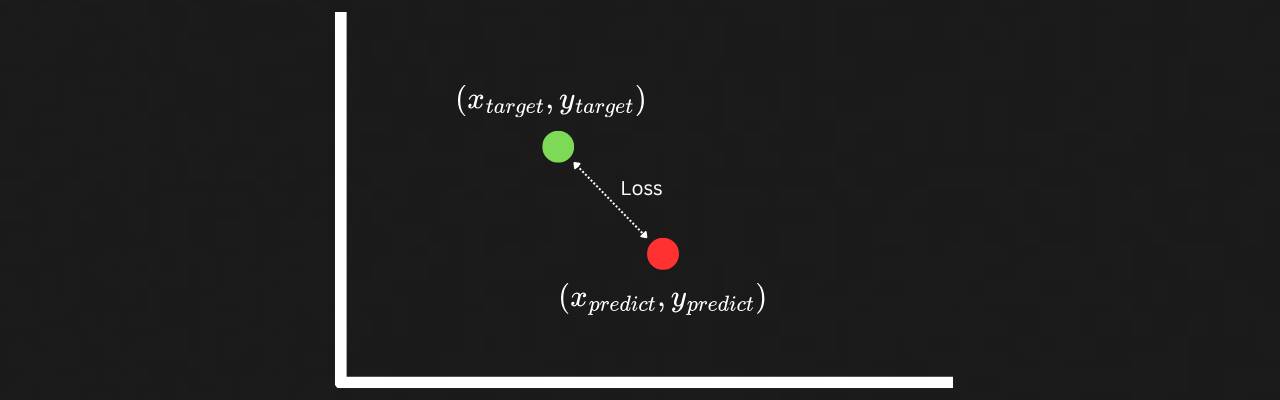
So how do we find this magic combination of weights w₁ to w_m that gives the lowest possible value for the loss function? This is where the concept of Gradient Descent comes into play. To better understand this, consider a scenario where our perceptron has only two inputs, and therefore, two weights, w₁ and w₂. For all possible values of these weights and a given input, we get the following loss landscape, which depicts the value of the loss function for any given combination of w₁ and w₂. Red indicates higher values of loss, while blue indicates low values of loss for the given set of weights.

Sample Loss landscape for all possible values of weights w₁ and w₂

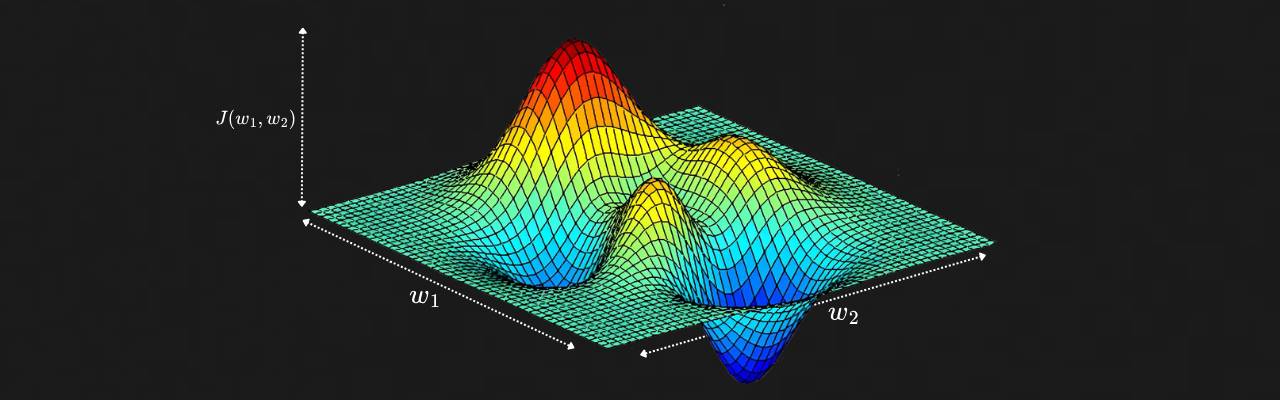
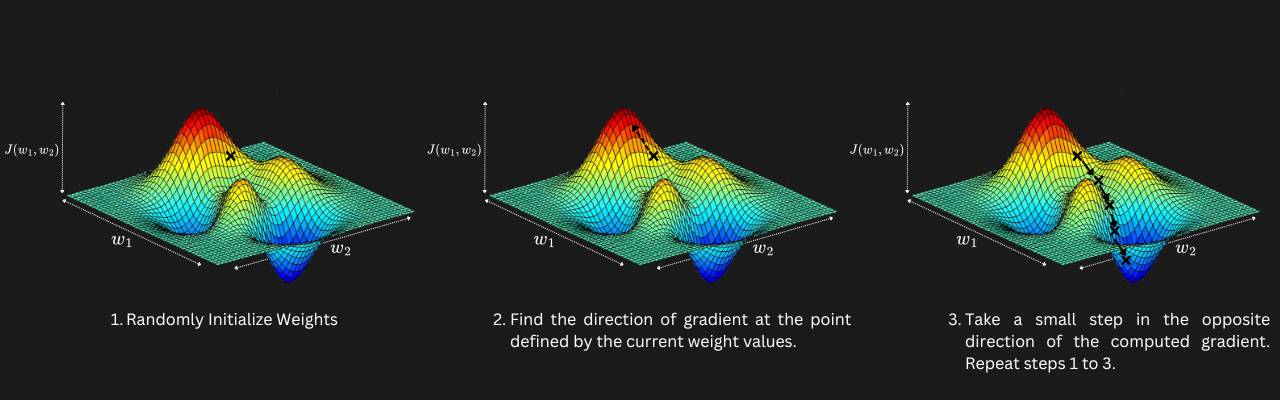
If you plan to brute-force your way to find the ideal weight values by testing all possible permutations and combinations, it would take forever — even for this simple situation with just two weights. Instead, what we can do is to select a random value for all weights. With these randomly initialized weights, we obtain a point on the loss landscape.

The next step is to calculate the gradient of the landscape at this point, i.e., we compute the derivative of the loss function with respect to the initialized weights. This tells us, for that given point, the direction in which the slope of loss is increasing. By taking the negative of this (the opposite direction), we find where the slope is decreasing, which is what we need, as we are trying to reach a region of lower loss. We now take a small step in the direction of lower loss, update our weights, and repeat this process until we reach a region of sufficiently low loss.

Steps in Gradient Descent

This can be represented in the following equation:

Gradient Descent Equation

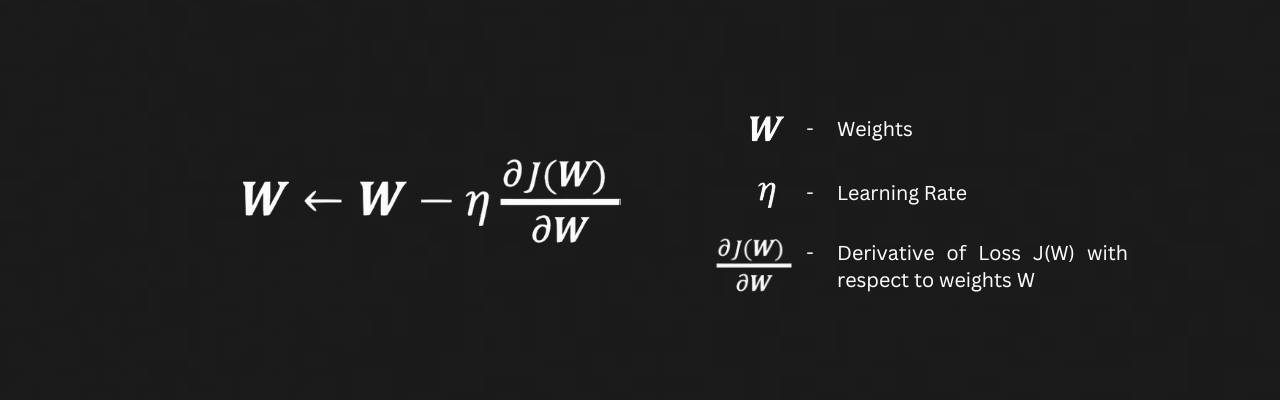
We update our weights by taking a small step, set by the learning rate η, in the opposite direction of the gradient of the loss function J(W). Moving in the negative gradient direction helps us find areas with a lower loss, guiding us toward a minimum for the current weights W.

Gradient Descent vs Stochastic Gradient Descent(SGD)?

If you have spent some time in the AI space, it’s most likely to have come across these terms. So what is different between these 2 types of gradient descent?

When it comes to generic gradient descent, all available training examples are used, and the average gradient dJ(W)/dW of all examples is utilized to make one single gradient update. In contrast, with SGD, we instead take a single example from our training set, compute the cost for that example and update the model’s parameters based on this single example’s gradient. This process is repeated for each example in the training set.

Gradient Descent vs Stochastic Gradient Descent

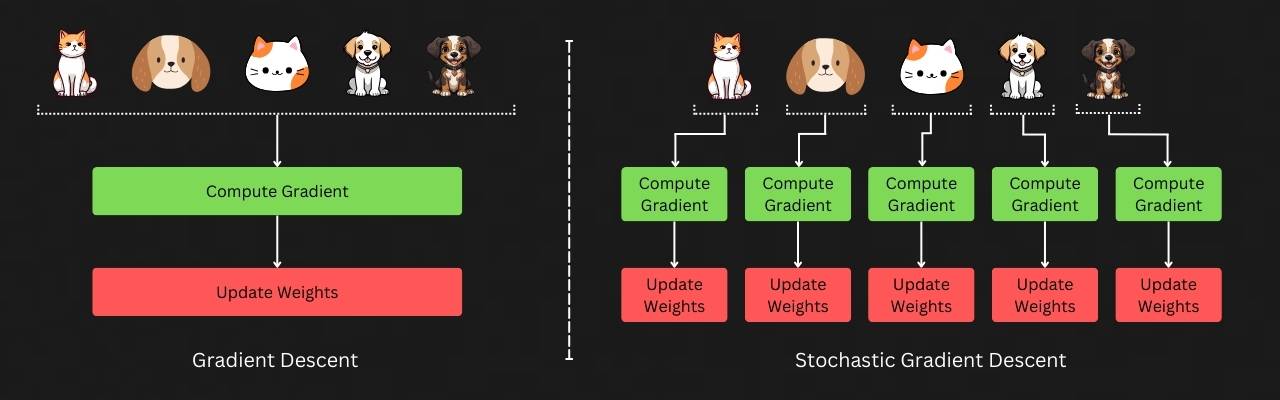
The reason this is called “Stochastic” is because using a single example instead of the entire dataset makes the process of descending the loss landscape quite noisy. However, this noise turns out to be a blessing in disguise, as it helps our neural network skip areas of bad or steep local minima, preventing it from getting stuck at so-called “saddle points”. Another benefit is that since gradients are updated for each data point in the training dataset (instead of waiting to process the entire dataset), we can train the model much faster.

Gradient Descent vs Stochastic Gradient Descent (Loss Curve)

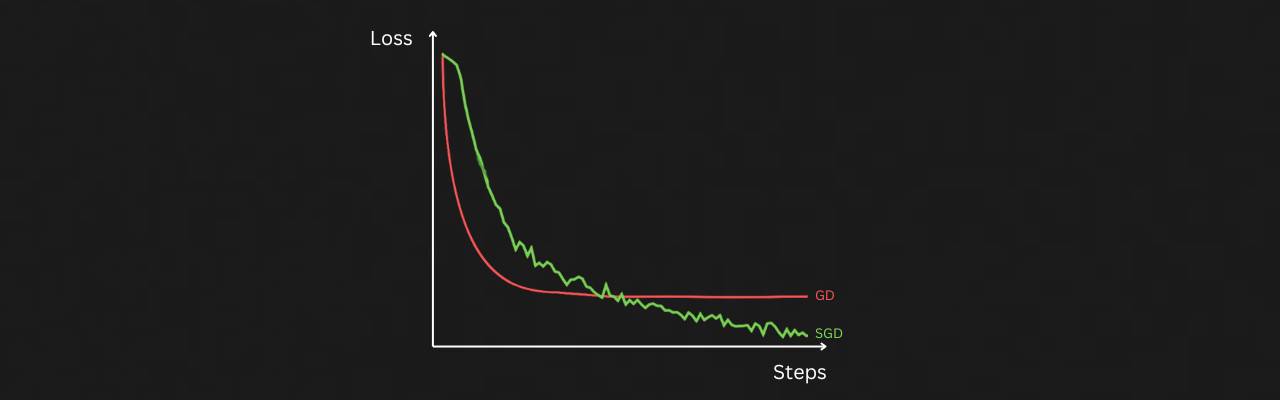
This video from the channel Visually Explained provides a good overview of why SGD is effective. Typically, what is implemented in practice is that we split our dataset into batches, each containing a small subset of the training data, and gradient updates are performed based on the contents of these batches. This is where the batch size parameter, which we commonly see in deep learning libraries, comes into play.

Caution regarding Setting the Learning Rate!

The learning rate η, decides how large of a step we need to take in the direction of the negative gradient. One might think that setting a large enough value of η could help us reach a local minimum with fewer steps. However, if it’s too large, we might jump over the minimum region of the loss landscape entirely and land in a non-ideal location, causing us to oscillate back and forth.

Alternatively, if the learning rate is very low, it may take a long time to reach the minimum region. We could also become trapped in a local minimum, unable to make a large enough step to escape and progress toward the ideal global minimum in the loss landscape. For each specific use case, network architecture, and weight initialization, the learning rate must be balanced — neither too high nor too low.

Effect of Non-Optimal Learning Rate on Training

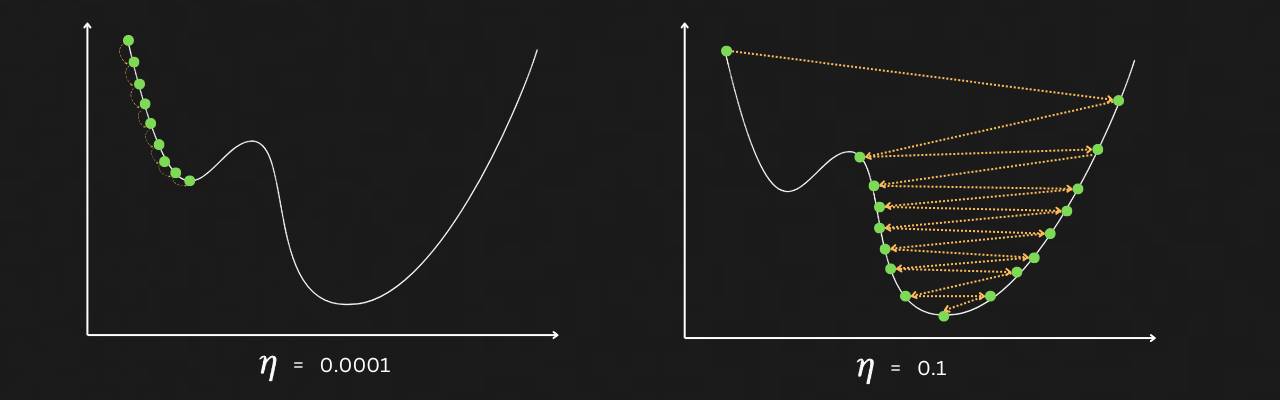
Finding the optimal learning rate has traditionally involved trial and error, as the ideal value can vary across different use cases. Learning rate schedulers are typically used during training complex neural nets as they dynamically adjust the learning rate throughout different training phases, improving weight updates for the task at hand. Techniques like the LR-Range Test can also help determine a good starting learning rate for neural networks.

Some Math before Code

Let’s establish the ground rules first. Here are the specifications for what we will code.

1. A single perceptron (neuron) with an input length of N.
2. One output.
3. Activation functions: linear, sigmoid, ReLU.
4. Mean Squared Error (MSE) loss.
5. Stochastic Gradient Descent with a batch size of 1.

The important part is where gradient descent occurs. How do we write the derivative of our cost function (or loss) with respect to our weights as code? Most articles I’ve encountered take a shortcut at this stage and use the loss function directly to compute the gradient. However, I’d like to take the hard route, even for this teensy tiny perceptron.

Revisiting the equation for gradient descent:

where W is the set of N weights (corresponding to N inputs), J(W) is the cost function, η is the learning rate. What do we have for J(W)? As mentioned in the specifications above, it’s going to be the MSE loss (mean-squared error).

Wait, this does not look like the equation of MSE… Where did the denominator go? Since we are using ‘Stochastic’ gradient descent, the denominator becomes ‘1’ as only one example is considered at a time. ŷ stands for output predicted by the perceptron and y, the expected output. ŷ can be further expanded as the output of the activation function (a) applied to the weighted sum of inputs (z) along with the bias (b).

Time to refresh some calculus, starting with the weight w₁. The gradient descent equation for this weight looks like this:

Applying chain rule, the equation for derivative can be broken down like this:

where,

With all these partial derivatives applied, the final equation for a single weight w₁ becomes:

The same is applied for the remaining weights w₂ to w_N. Check this amazing video by 3b1b for an animated intuition of the above calculus.

Code Implementation

With the technical know-how out of the way, lets check on how to implement this. You can find the code in the following notebook.

The perceptron class is defined as such:

class Perceptron:
    def __init__(self, input_size: int, learning_rate: float, activation_function:dict):
        self.input_size    = input_size
        self.learning_rate = learning_rate
        
        self.weights    = [random.uniform(-1, 1) for _ in range(input_size)]
        self.bias       = random.uniform(-1, 1)
        self.activation = activation_function
    
    def train(self, inputs, targets, epochs,verbose=False):    
        if len(inputs) != len(targets):
            raise ValueError('Inputs and targets must be of the same length')
        
        for _ in range(epochs):
            for input_vector, target in zip(inputs, targets):
                output              = self.forward_pass(input_vector)
                weighted_sum        = output['weighted_sum']
                activated_output    = output['activation']
                activation_gradient = self.activation['activation_diff'](weighted_sum)
                loss                = (activated_output - target[0]) ** 2

                if verbose:
                    print(f"Loss: {loss:.7f}, Weights: {self.weights}")

                # Update weights
                for i in range(self.input_size):
                    self.weights[i] -= self.learning_rate * (input_vector[i] * activation_gradient * (activated_output - target[0]))
                
                # Update bias
                self.bias -= self.learning_rate * (activation_gradient * (activated_output - target[0]))
            
        print(f"Final loss: {loss:.7f}, Weights: {self.weights}")
    
    def forward_pass(self, input_vector):
        if len(input_vector) != self.input_size:
            raise ValueError('Input vector size does not match expected input size')
        
        weighted_sum = sum(x * w for x, w in zip(input_vector, self.weights)) + self.bias
        activated_output = self.activation['activation'](weighted_sum)
        return {'weighted_sum': weighted_sum, 'activation': activated_output}

First, the class initialization.

def __init__(self, input_size: int, learning_rate: float, activation_function:dict):
    self.input_size    = input_size
    self.learning_rate = learning_rate
    
    self.weights    = [random.uniform(-1, 1) for _ in range(input_size)]
    self.bias       = random.uniform(-1, 1)
    self.activation = activation_function

Here we take take input_size which is the number of inputs passed on to the perceptron, learning_rate and also the activation function. input_size is used to randomly initialize the weights and bias for the perceptron with random float numbers between -1 and 1. activation_function is taken as a dict of 2 functions, the activation function and its derivative’s function.

# Sigmoid Activation and its derivative

def sigmoid(x): return 1 / (1 + math.exp(-x))
def sigmoid_diff(x): return sigmoid(x)*(1-sigmoid(x))

# Linear Activation and its derivative

def linear(x): return x
def linear_diff(x): return 1

# ReLU Activation and its derivative

def relu (x): return max(0,x)
def relu_diff(x): return 0 if x<=0 else 1

Up next is the forward propagation function. This is responsible for taking inputs, calculating its activated weighted sum and returning the result

def forward_pass(self, input_vector):
    if len(input_vector) != self.input_size:
        raise ValueError('Input vector size does not match expected input size')
    
    weighted_sum = sum(x * w for x, w in zip(input_vector, self.weights)) + self.bias
    activated_output = self.activation['activation'](weighted_sum)
    return {'weighted_sum': weighted_sum, 'activation': activated_output}

And finally the train function which takes in a list of inputs and targets which is then used to train the model via gradient descent. Epochs refer to the total number of times we iterate through the entire dataset.

def train(self, inputs, targets, epochs,verbose=False):    
    if len(inputs) != len(targets):
        raise ValueError('Inputs and targets must be of the same length')
    
    for _ in range(epochs):
        for input_vector, target in zip(inputs, targets):
            output              = self.forward_pass(input_vector)
            weighted_sum        = output['weighted_sum']
            activated_output    = output['activation']

            activation_gradient = self.activation['activation_diff'](weighted_sum)  # dz/da
            loss                = (activated_output - target[0]) ** 2

            if verbose:
                print(f"Loss: {loss:.7f}, Weights: {self.weights}")

            # Update weights
            for i in range(self.input_size):
                self.weights[i] -= self.learning_rate * (input_vector[i] * activation_gradient * (activated_output - target[0]))
            
            # Update bias
            self.bias -= self.learning_rate * (activation_gradient * (activated_output - target[0]))
        
    print(f"Final loss: {loss:.7f}, Weights: {self.weights}")

Winding Up!

The notebook includes implementations for several examples, such as different functions and varied inputs. It also demonstrates interesting scenarios like exploding and vanishing gradients. What we covered here is just a single perceptron, but the concept remains the same when using neural networks, where instead of a single perceptron, we might have layers of multiple perceptrons arranged in specific ways. The underlying concept is fundamentally the same.

Another thing to note is that all these computations are typically implemented as matrices, which are much more effective for handling weight updates for millions or billions of weight parameters. These can be easily managed by computing accelerators such as GPUs. With that, I’ll wind up this post for now. Tschüss!

References

• Intro to Deep Learning
• Gradient Descent From Scratch
• A Simple Introduction to Gradient Descent
• Backpropagation Calculus - 3b1b